[ DATT-A9D > 地形にカンパイ > 地形の特徴・地形の複雑度 ]
最終更新:2025年7月19日
地学といえば産総研。産総研の動画を見ながらも、目の前の「A列車で行こう9」というPCゲームの前に戻ってきて、いざ解析。
PCゲーム「A列車で行こう9」のゲーム画面では、プレーヤーが開発に取り組むゲーム内の空間(「マップ」)全体を俯瞰する「サテライト」と呼ばれる子画面が用意されている。標高によって色分けされ、建物や線路などが種類ごとに色分けされて示される。ゲーム中に表示させておくことによって、列車がどこを走っているという運行状況を一覧したり、クリックして目的の地点にすばやく移動することに使える。さらに、「サテライト」を上を北に固定する設定と、視点(※3DCGでいう「カメラ」)の向きにあわせて回転させる設定とを切り替えることができ、列車に乗車している気分で「マップ」を鑑賞できる「車窓モード」(※なぜか「車窓」とはいうが運転台からの前方のビュー)で「サテライト」を回転させれば、カーナビのような感覚が楽しめる。
「A列車で行こう9」の「サテライト」は、セーブ・ロードの画面ではゲームの進行状況を示すサムネイルの役割を持たされている。公式ガイドブック(全4冊)の「マップ攻略」でも「サテライト」の画像が掲載され、文字では「産業構成比」「都市情報」「資金」「交通施設」と「主な施設」が列挙されている。しかし、そのマップがどんな地形なのかを数量的に示すには至っていない。あくまで「サテライト」の画像(標高を色分けして示したもの)を見よということにされている。人の目で画像を見ているだけでは『データ』ではない。
「A列車で行こう9」というゲームの中ではなぜか「サテライト」という呼びかたではあるが、これは地形図である。建物や線路などがない状態では、マップ全域の土地の高低や起伏を正確かつ完全に読み取ることができる。ここでは、この「サテライト」の画像をキャプチャ(※Windowsの通常の操作である[Print Screen]キーを使用)して『データ』をつくってみよう。
※諸般の事情により、セーブ・ロードの画面に表示される256×256ピクセルの状態でキャプチャする。「建造物初期化」を実行しておく。こんなことをしなくても済む「ハイトマップのエクスポート」が追加されることに期待しておく。

▲スクリーンショットからトリミングして、このような256×256ピクセルのPNG画像を用意してほしい
| height | pixels |
|---|---|
| 230 | 8 |
| 220 | 14 |
| 210 | 24 |
| 200 | 37 |
| 190 | 34 |
| 180 | 55 |
| 170 | 118 |
| 160 | 122 |
| 150 | 198 |
| 140 | 247 |
| 130 | 334 |
| 120 | 443 |
| 110 | 536 |
| 100 | 686 |
| 90 | 728 |
| 80 | 774 |
| 70 | 824 |
| 60 | 966 |
| 50 | 1061 |
| 40 | 1111 |
| 30 | 1282 |
| 20 | 1513 |
| 10 | 1497 |
| 0 | 32523 |
| -3 | 3364 |
| -10 | 2099 |
| -20 | 1896 |
| -30 | 1240 |
| -40 | 728 |
| -50 | 570 |
| -60 | 594 |
| -70 | 804 |
| -80 | 9106 |
| サンプルデータ |
|---|
| マップコンストラクションで作成したマップの「サテライト」の画像のピクセルの色を読み取って数値化したデータ |
| その他のマップについてはこちらとこちらから |
このままでは「サテライト」の画像と同じく、割合(面積)を見て何か言うことしかできない。地形の特徴をあまさず表現する「多変量データ」にしていこう。1つ1つの「変量」は、アンケートの設問のようなものと思ってもよい。「あなたはどんな人ですか」と聞かれても答えに窮すが、具体的な設問が9つあって順番に答えると「こんな人です」ということが浮かび上がるイメージだ。
ここでは「このマップはどんな地形ですか」ということが知りたいので、「サテライト」の画像を人の目で見たときに読み取ることができるさまざまなことがらを、地形データ(ハイトマップ)を使って表現していく。このデータには「平面の座標」と「標高」という、実質的に2種類の情報しか含まれていないので、この情報から言えることだけを言うことになる。

▲色はこちらを参考にした
| color | pixels | ||
|---|---|---|---|
| #585757 | 5182 | 7.9% | 山 |
| #878787 | 4420 | 6.7% | |
| #b4b4b4 | 3010 | 4.6% | |
| #dbdcdc | 35887 | 54.8% | 平地 |
| #1bacfa | 7931 | 12.1% | 水面 |
| #1293f9 | 9106 | 13.9% |
これらを組み合わせ、なるべく重複しないよう考えたのが、以下の9つの変量である。とりうる最大値で割る「正規化」をしておこう。
※すべて文字で書いていることをお許しいただきたい。「/」は割り算の記号である。分数のように見て、「/」の左側を分子、右側を分母と思ってもらいたい。
【注意】このゲームでの「空間」は現実とは異なり、“地球の丸み”がない。現実の地図(地理院地図)やGISとの間でのデータ交換などは行なわせないことを強く推奨する。ここは数学らしく取り組むことに徹し、このゲームでの「空間」の(数学上の)表現に沿って、いわば『このゲーム限りのGIS』を自作するような取り組みをさせたい。その上で、現実の地図やGISにおける実務的な種々の工夫や計算上の注意などにつなげてほしい。

フリーの統計解析環境「R」を用いても算出できるが、ここでは自作のツール「点・望・山(M243-11Y)」および「PAL8-CNV ~ぱるはちこんぶ~」を用いた。
ここで得た「V1」から「V9」までの各変量間における相関係数行列を以下に示す。当然ながら「V7」「V8」「V9」の3変量は互いに相関係数が高い。次に「V2」と「V6」の相関係数が高い。「V1」とほかの8変量との間では、極端に低い相関係数は出ない。(「V1」「V5」「V8」の間で互いに相関係数が高いと見ることもできる。)「V7」「V8」「V9」の3変量と、ほかの「V1」を除く5変量との間では、「V5」と「V8」、および「V3」と「V7」の相関係数が高い。一方、「V5」と「V7」の間では相関係数が最も低い。
| V1 | V2 | V3 | V4 | V5 | V6 | V7 | V8 | V9 | |
| V1 | 1 | ||||||||
| V2 | -0.312 | 1 | |||||||
| V3 | -0.367 | 0.149 | 1 | ||||||
| V4 | 0.485 | -0.369 | 0.485 | 1 | |||||
| V5 | -0.603 | -0.054 | -0.127 | -0.566 | 1 | ||||
| V6 | -0.191 | 0.769 | 0.277 | -0.113 | -0.263 | 1 | |||
| V7 | -0.246 | -0.285 | 0.456 | 0.302 | -0.006 | -0.235 | 1 | ||
| V8 | -0.522 | -0.027 | 0.226 | -0.31 | 0.554 | -0.216 | 0.454 | 1 | |
| V9 | -0.425 | -0.089 | 0.392 | -0.018 | 0.267 | -0.228 | 0.836 | 0.824 | 1 |
次に、「R」の「rpart」を使って「回帰木」を作成した。
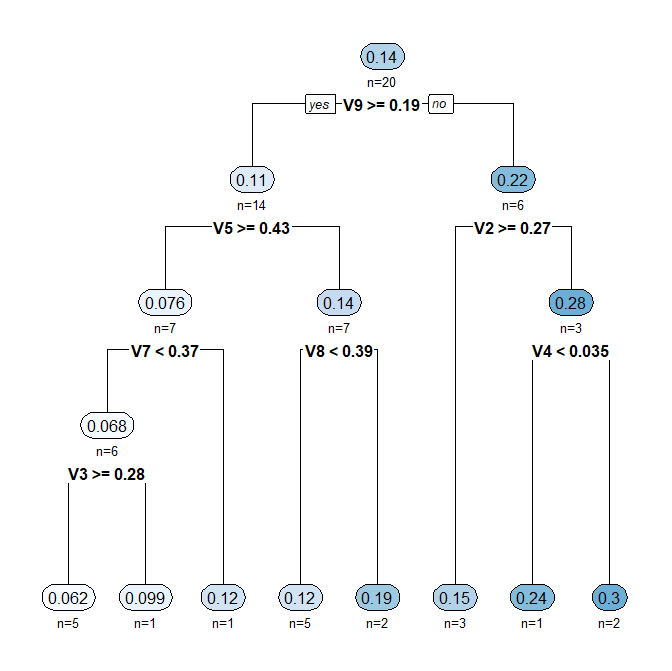
「V2」から「V8」までの変量を使って「V1」を説明する回帰分析の結果を「木」のかたちで示したものだ。最下段で8つに分かれる。これを左から(「V1」が小さい順に)「Type A」「Type B」「Type C」「Type D」「Type E」「Type F」「Type G」「Type H」と便宜的に呼ぶこととし、地形の特徴とした。この8つの中では、「V1」が小さい順のほかに順序はない。
「回帰木」は、(1)すでによくわかっているデータ(※1)を使って作成し、(2)よくわからないデータ(※2)が「木」のどこに分類されるか(すでによくわかっているデータのどれと似ているか)を調べるという使い方をする。
※1 「トレーニングデータ」「正解データ」「教師データ」などと呼ぶ。
※2 「テストデータ」「学習に用いないデータ」などと呼ぶ。
ここ(※自作のツール「点・望・山(M243-11Y)」)では、この(1)すでによくわかっているデータとして、このゲームに搭載された機能である「地形の自動生成」を使用して生成した地形データの中から、人の目で見て選んだ20個の地形データを使用した。

※「回帰木」の最下段の通りに並べた。なお、「回帰木」の最下段の枠の中の数字は、そこに分類されたデータにおける「V1の平均」である。「木」のかたちで表示する都合上、「V1」の大小が入れ替わって並んでいる部分もある。
※「V1」から「V9」までの変量は、この数字の順に思いついたわけではない。なるべくプレーンなものを前のほうに、もはや屁理屈ではというようなものを後ろのほうに並べた。そのようにして「V1」になったものを、被説明変数(目的変数)にすることにしたという順番である。
ここで「V1」という変量だけを単独で見ることを地形の複雑度と呼ぶこととした。「V1」の値を対数的に5つの区間に分け、低いほうから「Poor」「Average」「Good」「Excellent」「Too Complicated」というラベル(値の区間の名前)を与えた。
ゲームとしてのプレイアビリティは、地形の複雑度が「Good」なら問題なく、「Excellent」なら特別に優れ、そのほかは「Good」より劣ると判断してよい。「プレイアビリティが低い(線路や建物の配置の自由度がなさすぎるかありすぎる)」ということは『難易度が高い』(考えることやすることがたくさんある)ということであり、決して「つまらない」とか「取るに足らない」とは限らない。もちろん、マップのよしあしは地形の特徴と一体で考えるべきもの。地形の特徴と地形の複雑度が意味のあるかたちでつりあっていれば楽しい、つりあっていなければ楽しくない、と考えるとよい。
| 地形の 特徴 | 地形の 複雑度 |
V1 | V2 | V3 | V4 | V5 | V6 | V7 | V8 | V9 | 平地 (%) |
水面 (%) |
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ひしめきM | Type D | Good | 0.12 | 0.05 | 0.35 | 0.12 | 0.31 | 0.20 | 0.73 | 0.16 | 0.45 | 32.5 | 5.4 |
| エアポートM | Type D | Good | 0.14 | 0.08 | 0.46 | 0.11 | 0.31 | 0 | 0.38 | 0.15 | 0.27 | 53.3 | 8.2 |
| あかりM | Type D | Average | 0.06 | 0.33 | 0.44 | 0.04 | 0.43 | 0.40 | 0.39 | 0.15 | 0.23 | 52.2 | 33.4 |
| メトロポリタンM | Type D | Excellent | 0.17 | 0.06 | 0.30 | 0.07 | 0.24 | 0.16 | 0.48 | 0.15 | 0.31 | 55.7 | 6.1 |
| タ陽M | Type D | Poor | 0.04 | 0.13 | 0.49 | 0.05 | 0.36 | 0.40 | 0.53 | 0.32 | 0.42 | 70.8 | 13.0 |
| エキスパァM. | Type E | Poor | 0.03 | 0.31 | 0.29 | 0.02 | 0.12 | 0.52 | 0.36 | 0.58 | 0.44 | 57.2 | 31.0 |
| 一級河川の川リバーM | Type D | Good | 0.12 | 0.09 | 0.46 | 0.14 | 0.28 | 0.17 | 0.51 | 0.26 | 0.38 | 44.0 | 9.0 |
| ゆだM | Type D | Good | 0.13 | 0.00 | 0.55 | 0.22 | 0.27 | 0 | 0.41 | 0.04 | 0.23 | 35.8 | 0.4 |
| ネオン橋ブリヂM | Type H | Good | 0.09 | 0.05 | 0.39 | 0.06 | 0.46 | 0.16 | 0.15 | 0.13 | 0.06 | 68.9 | 5.0 |
| かまちM | Type H | Average | 0.06 | 0.02 | 0.47 | 0.08 | 0.62 | 0.01 | 0.12 | 0.07 | 0.05 | 70.8 | 2.3 |
| 三日月島MV | Type D | Too Complicated |
0.35 | 0.33 | 0.57 | 0.17 | 0.08 | 0.40 | 0.27 | 0.19 | 0.23 | 20.9 | 32.6 |
| 10ヴォスM | Type F | Excellent | 0.17 | 0.34 | 0.30 | 0.03 | 0.24 | 0.07 | 0.04 | 0.11 | 0.07 | 47.8 | 34.1 |
| ドリームM | Type A | Poor | 0.04 | 0.08 | 0.49 | 0.03 | 0.58 | 0.16 | 0.29 | 0.59 | 0.39 | 82.9 | 7.7 |
| マリネ屋M | Type F | Average | 0.06 | 0.42 | 0.31 | 0.01 | 0.61 | 0.19 | 0.21 | 0.44 | 0.12 | 50.7 | 41.7 |
| かけはM | Type D | Average | 0.07 | 0.10 | 0.66 | 0.29 | 0.00 | 0.20 | 0.53 | 0.14 | 0.34 | 17.1 | 9.8 |
| スタァライト川崎M | Type D | Average | 0.06 | 0.01 | 0.56 | 0.22 | 0.14 | 0.01 | 0.28 | 0.16 | 0.20 | 40.6 | 1.0 |
| ストライドM | Type H | Average | 0.07 | 0.15 | 0.72 | 0.25 | 0.34 | 0.00 | 0.09 | 0.06 | 0.06 | 38.1 | 15.0 |
| ハーイおばけM | Type E | Poor | 0.05 | 0.39 | 0.45 | 0.08 | 0.12 | 0.43 | 0.34 | 0.50 | 0.42 | 33.7 | 39.5 |
詳細は以下のページに譲る。
多変量解析のおもしろさを伝える題材として「卵の形は産む数や環境要因、巣の特徴などと関係がない一方で、「ハンド・ウイング指数」が最も高い、つまり最も効率的に飛べる鳥は、卵の非対称性または楕円率が最も高いことがわかった」(2017年6月27日)がおすすめである。理科の単元にとらわれ、いわゆる重回帰分析だけで終わるような展開では物足りない。
Excelと高校の数学だけでできることしかしないという展開には感心しない。「地理探究」などの探究型学習に関連し、応用地質・みずほ情報総研・インキュビット「複数の地形的特徴から土砂災害の危険性がある地域を抽出するAIモデルを開発」(2019年9月2日)といったニュースを漠然と見るのでなく、具体的な計算や特徴量の用意のしかたをイメージさせる必要がある。ここでは人の目で見て人の頭で考えて(やっとのことで)9つの変量を得ているが、これを自動的に無理やり見つけてくれるのが「ディープラーニング」であるという説明のしかたもできる。
いわゆる空間統計学の教科書に則りながらの、工学の現場で通用する実際的な計算法については関知しない。それは工学であって理数探究ではない。プロの道具をおもしろがって勝手にいじるようなことはさせない。プロはそれをものすごく嫌う。
わたしたちは基本的に「R」を使うほかない。例えばExcelVBAやPythonでじぶんでコードを書く(生徒に書かせる)ためには、これ(黒板と紙に手で書ける数式)をぜんぶ自力で書いて説明して他人を納得させることができないといけない。
西陣織で星月夜。このページで「回帰木」という呼び方で紹介しているものは「CART法」という名前で発表されたもので、その考案者はのちに「ランダムフォレスト(Random Forest)」を提案している。特定の分野では「決定木」「決定木分析」と呼んできた(すべて手作業で作成する場合すら含む)が、わたしたちがこれから取り組む「理数探究」としては、数学と統計学の諸概念や用語に照らして一般化した呼び方である(応用には踏み込まない)「回帰木」という名前を使うことが強く望まれる。「CART法」は、与えた多変量データを総当たりで調べ尽くしてくれるアルゴリズムである。影響の大きいものだけを選択的に見ていく「変数選択法」による重回帰分析や手作業の混ざる(昔の、あるいは文系の)「決定木分析」よりも、はるかにエレガントな方法であるといえる。半端な形ではあるが「ランダムフォレスト(Random Forest)」に通じてゆく、機械学習の入り口と捉えさせるようにしたいものである。よりクラスタリングに片足を乗せた実用的な方法として「ID3」「C4.5」の系統があるが、折衷的な方法であるので「理数探究」で取り上げるのは妥当でないと考えられる。幾何学へのいざないとしては「最小全域木(MST)」「アルファシェイプ(α-shape)」「凸包(convex hull)」などにつなげられるだろう。
(初版公開:2020年5月29日、改訂:2022年5月11日)
※ゲーム内の地形データの著作権はゲームソフトのメーカーに帰属すると思われます。
ARXあげます万葉(42483) All Rights Reserved. ©2018-2025, tht.