[ DATT-A9D（ＡＲＸのつまみソース） > データで遊ぶ > 府中のメソッド ]

PCゲーム「A列車で行こう9」で遊びながら学ぶ、Rのハローワールド。（最終更新：2025年7月6日）

府中のメソッド ～ノエルがいっぱい～

• ゲームのマップの「平地」に「路線網」を無駄なく引きたい
• アルゴリズムは既成のものをなるべくそのまま使う
• 「片栗粉Ｒ」と同様にして読み取ったマップの高度（標高）から「平地」のみを抽出して使う

その他の地形についてはこちらから。
おもなシナリオマップについてはこちら。

Rのスクリプト

フォーラムの以下の記事で試行錯誤的に細切れに実行例を紹介していますので拾い読みしてください。

• まずはゲームとして遊ぶ：路線網はJR線のつもりで引いた・池のほとりに古代から国の役所が置かれたという歴史を想像した（『御池1400』）
• Rに読み込んでいろいろ試す（順不同のデモンストレーション）
• クラスタリングから最小全域木まで（ゲームとして遊んだ結果を正解データとみなしての実験という意識で）

この実験より前に（人手で）ゲーム内で引いた路線網（※上が北）
▲NMPC-L64で描いた図 （編集可能）	▲北部の水面は海とみなす ▲平地西側に大小2つの池あり ▲池と山の間のG地点を都心とする ▲都心Gを通る東西の幹線 ▲都心Gから山裾に沿って南下し隣町D ▲隣町Aから南下し池にあたり東進 ▲池と港に面した都市Hを通る貨物線 ▲隣町Fから都心Gへの高規格新線 ▲一級河川の川（駅K東）が街を分かつ ▲河口部の橋だけで凍結の未成線 ▲空港は隣町Aにあるものとする ▲貨物線IK間に卸売市場

• 「写真の想起による境界拡張の生起」日本認知心理学会第13回大会（2015年7月4日）
• 「画像イメージの記銘と想起における空書行動の有用性」日本認知心理学会第11回大会（2013年6月29日）

• 『多賀城1300』（2024年）
• 「小手指1800」（1972年）
• 「901系」と「STAR21」（1992年）
• 「JR大井工場」（1992年）

モチベーション

「A列車で行こう9」はゲームであるから、このようなイメージのもと、まずは思う存分に遊んでから、以下の「データを対象とした実験」に進む。「実験」と呼べるほど（化学や物理のような）厳格なものではないが、ゲームで遊んだ結果を一種の仮説とみなして、人手でゲームを遊んだときに出てくる結果をアルゴリズムでも出せないかともがくのである。人間のプレーヤーとしてはゲームの外側で上掲の参考画像のようなイメージ（表象・心像）というかたちの外部知識を持つ。「思う存分に遊ぶ」とは、人間のプレーヤーとしてベストを尽くす（多くの人がばらばらに遊んでも究極的には同じになっていく＝誰もが「これがベスト」と判断して選び取ってゆく＝一種の共通認識のようなものを獲得するまで遊ぶ）ことであり、でたらめに遊ぶということでも、ただ時間をかけさえすればよいというものでもなく、じぶんのこだわりにこだわるのも適当とはいえない。アルゴリズムによって人間のプレーヤーの行動をうまく模擬できれば、シナリオの自動提案やプレーのガイド機能、採点機能や、好みが似ているプレーヤーの推薦などに応用できる。

なお、CV（コンピューター・ビジョン）のデモンストレーションとして往年のレトロゲームを『AI（人工知能）えーあいかっこじんこーちのー』にプレーさせるものとは意味が異なることに注意。ゲームのデータをただの素材として使うのでなく、ゲームそのものの改善や進化につながる手法の開発（※企画やプログラミングという意味のゲームソフトの開発の手前の段階の要素技術の開発）を目指すつもりで臨もう。

k-means法を使おう

k-means（k平均法）は非常に応用の広い基本的なアルゴリズム。多変量解析やデータサイエンスの技法の1つとして習う人もいれば、画像の減色処理のアルゴリズムとして知る人もいる。ゲーム「A列車で行こう9」でも、k-meansを使ってみよう。

「平地」を抽出		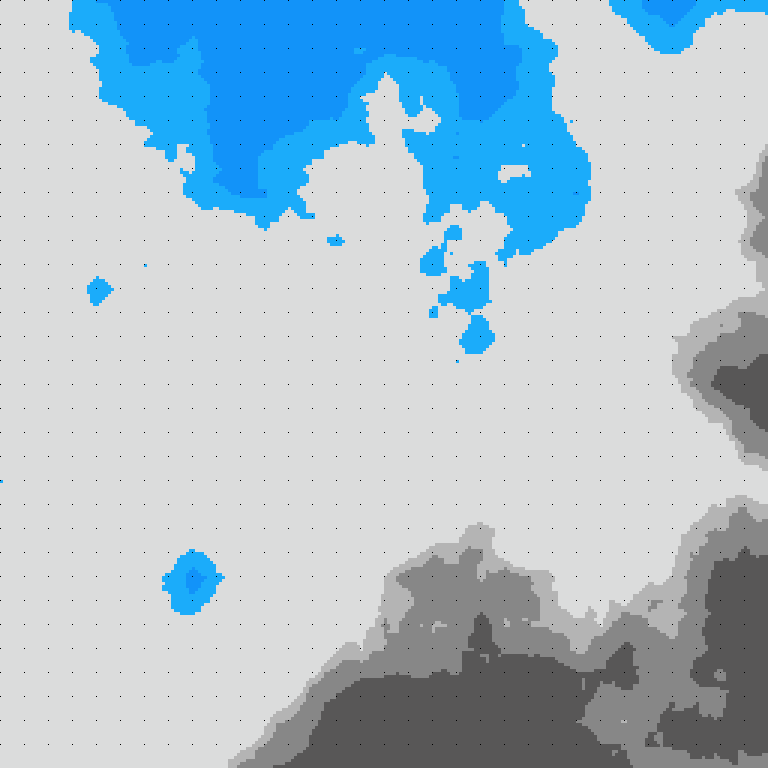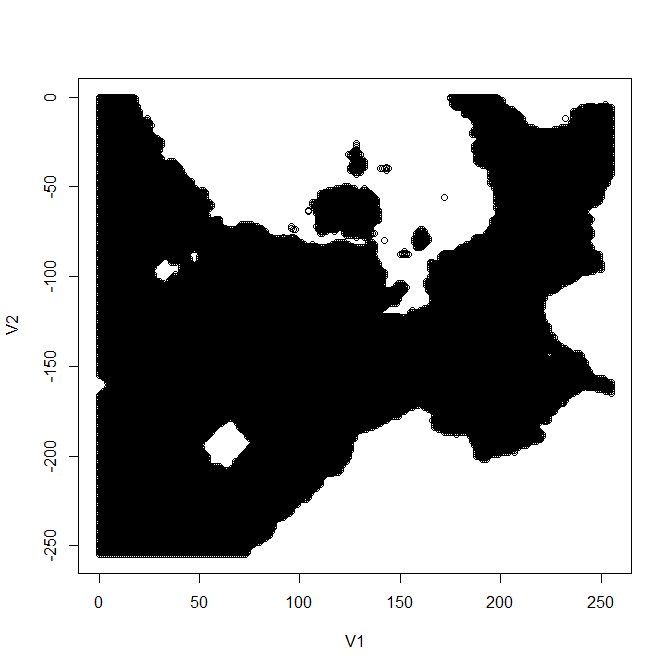TSVファイル
「平地」を分割 （k-means法）
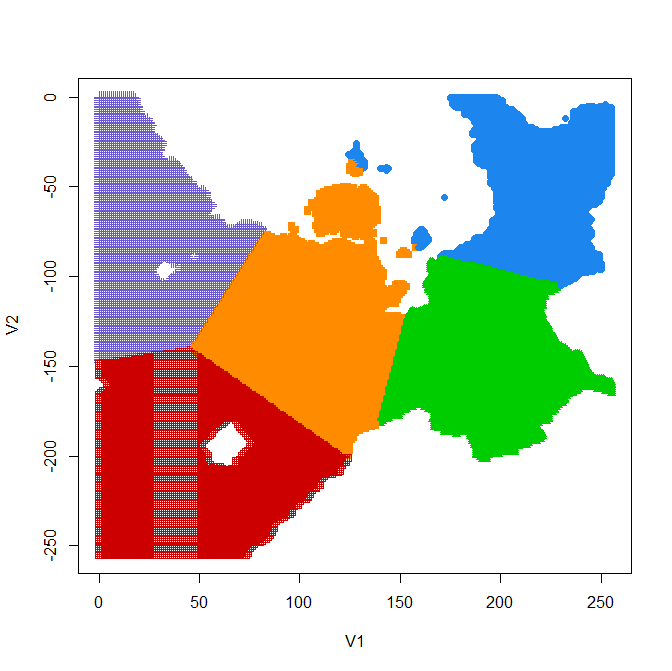	▲k=3（21+1）	▲k=5（22+1）
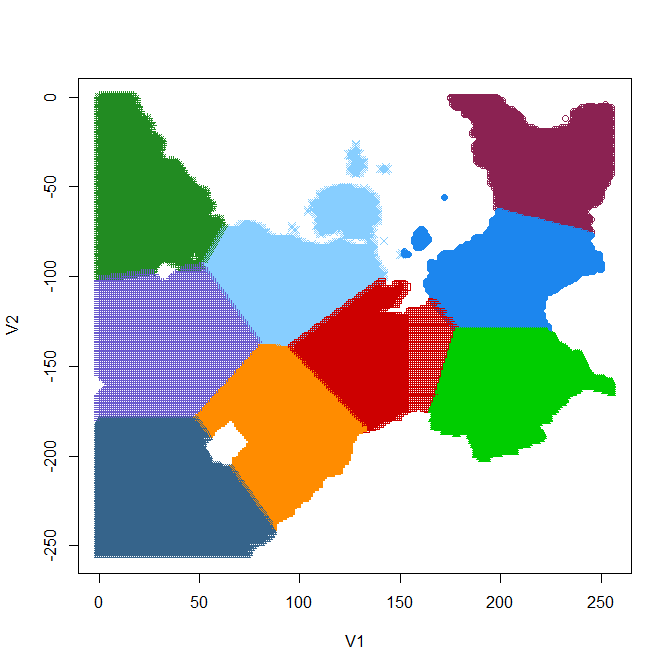
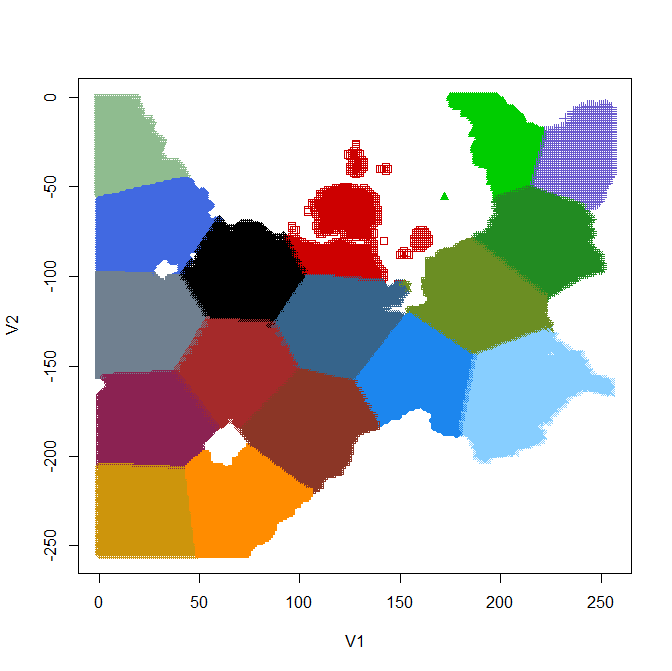
	▲k=9（23+1）	▲k=17（24+1）
「k=17」を使う ことにする ＆ クラスター3個を除外

ディスカッション

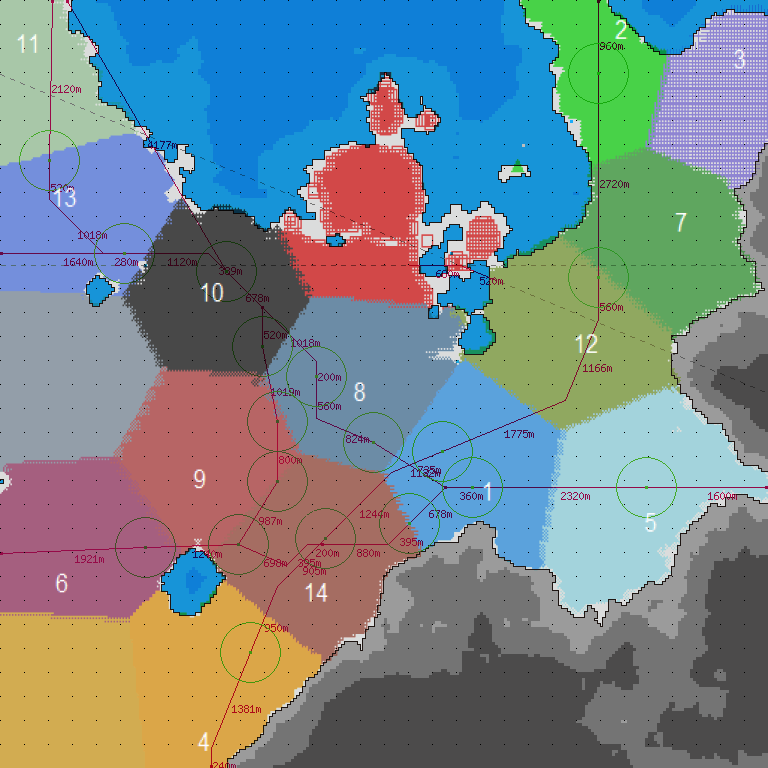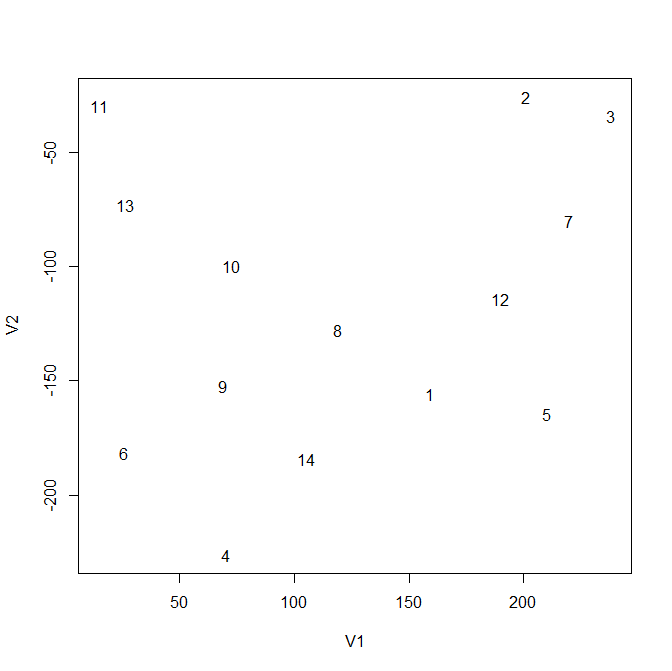
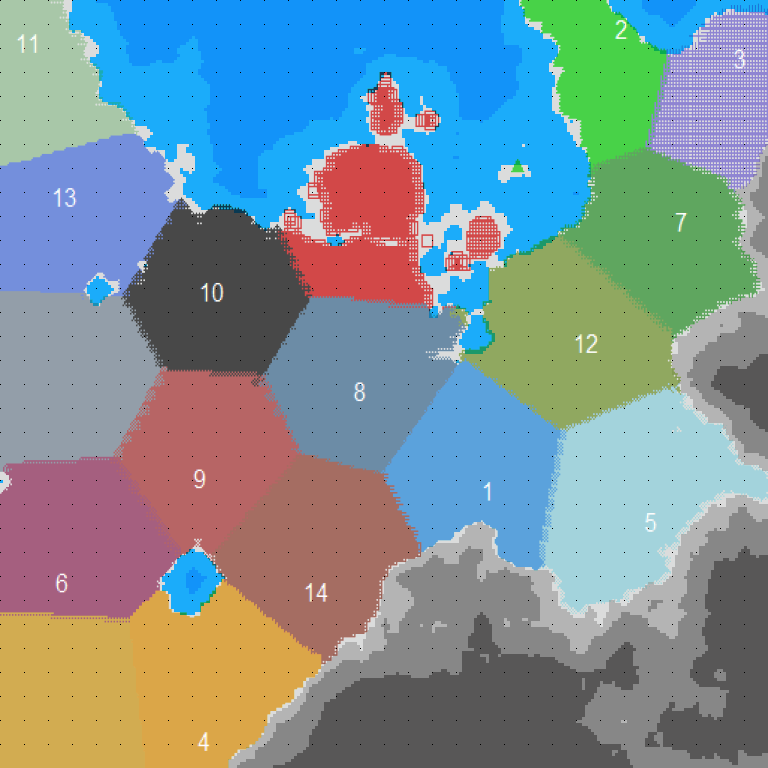
▲グラフィックソフトで重ねる （数字の位置がずれた）	▲この実験より前に（人手で） 　ゲーム内で引いた路線網 （との対応を見比べる）
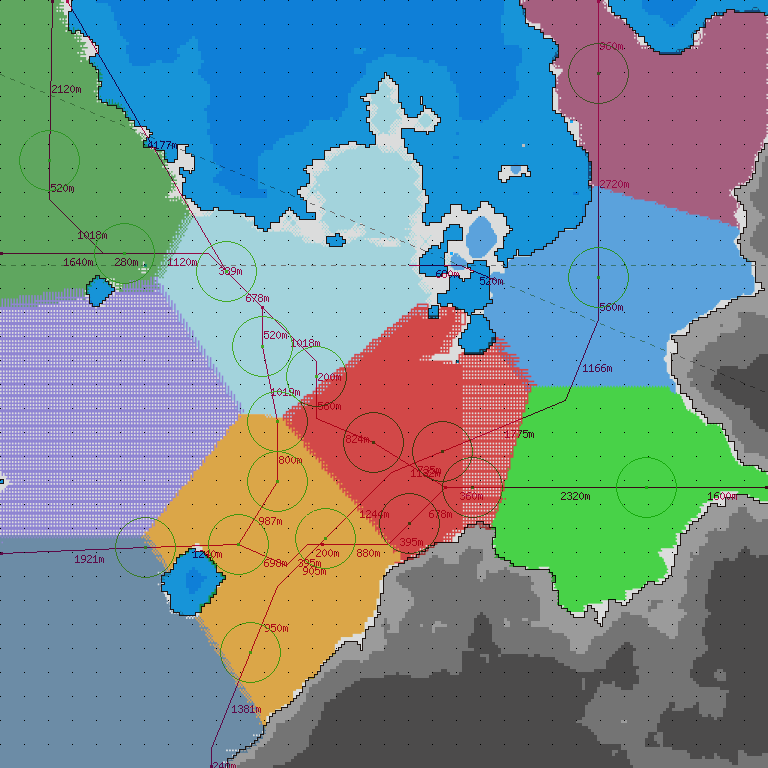▲この実験より前に（人手で） 　このマップにつけた町名 （との対応を見比べる）	▲k=9

• ゲームのマップに市街地や駅を初期配置する方法として「k-means法」が使えそうではあるが、自動ではクラスター数を決めかねるとわかった
• マップの全域に均等に駅が配置されると不自然であるのでランダムでもいいからいくつかのクラスターを除外するとよいのではないか
• 「地形の自動生成」を使用したマップであれば「地形の複雑度」という数字があるので、クラスター数の決定に使えそうという感触を得る
• この実験より前に（アルゴリズムを使わずに）考えた路線網や町名は、「k=9」の細かさで考えた部分と「k=17」の細かさで考えた部分の両方がある（場所によって細かさを使い分けている）
• 山と水面を除いた平地の部分を「k=17」で均等に分割することは、プレーヤーの直感的な地形の解釈とあまり反しない感じがする
• 均等に分割した領域（クラスター）の重心を駅の立地とみなすとき、駅を平面上で互いに等間隔の位置に置くことになる（路線を引いてから駅間距離を等しくするのでなく、平面上で駅を均等に配置する方法となる）
• 地域への駅の配置が最も公平となる配置（いわば駅勢圏という円を最密充填した状態）ではあるが、この配置（重心）で駅と駅を結べば最適な路線網ができあがるとは限らない（駅の平等な配置と路線網の効率はトレードオフ）

プレーの「分解能」

「A列車で行こう9」では、駅の建設には平らな土地が必要になる（※高架駅にする場合も土地が平らである必要がある）ことから、マップをどのように使っていくか（どのような路線網にするか）を考えるときは、主に「平地」を見ることになる。（※ある程度の面積がまとまって平らであるなら、標高が0mより高い「高台」も考慮に入れる。）

このときに、マップ全体の「平地」をどのような細かさ（※「分解能」ともいう）で見るかということが、「府中のメソッド」（クラスタリング）でいう「クラスター数」である。ここでは「地形の自動生成」の使用を前提とし、この機能で地形仮生成を実行するときに「地形の複雑度」というパラメータを指定するので、そこに依拠してクラスターの数を決められないかと考えた。

※「分解能」：顕微鏡や衛星写真と、それに類する各種計測器でいう言いかた。どのくらい小さな物体まで識別できますという「能力」をいう。

「地形の複雑度」は整数で指定する。アルゴリズムの説明は省くが、折り紙を折る回数のような意味合いの数字である。このことは「地形の複雑度」に5～9のような大きな数字を指定したときに顕著にわかると思う。せいぜい1～3が実用域だろう。この「地形の複雑度」は、3次元の地形データを上から平面的に見ての縦と横（xとy）それぞれに効くものである。（※高さ方向（z）に効かせるものは「起伏の複雑度」という別のパラメータになっている。）「地形の複雑度」に「2」を指定したとき、それは縦と横で、それぞれ折り紙を1回折るということになる。折った折り紙を広げてみると、縦と横の折り目によって「マス目」ができている。「地形の複雑度」が「2」のとき、縦と横がそれぞれ折り目を境にして2つに分かれ、平面として見れば4つに分かれているということになる。「地形の複雑度」が「2」のときのいわば分解能（※いわば「画素数」）は「4」になる。「地形の複雑度」を「3」にしたときは2回折って4つに分かれ、縦と横がそれぞれ4つだから、全体は16個のマス目になる。「4」にしたときは、いくつになるだろうか。（※「地形の複雑度」が「1」のときは0回折るととらえた。）

ただ、これでは細かすぎるという感覚があるのも事実だ。ここでは「地形の複雑度」から着想を得たが「地形の複雑度」そのものにはこだわらず、なんかそんな感じの折り紙を折ってから広げてできるマス目のような数えかたで「クラスター数」を決めたいと思った。

A4の紙を封筒に入れるときの折り方がある。「地形の複雑度」の数え方で数えてしまうと、「3つに折る」という状態を飛ばして数えてしまうことになる。そういうところを考えているうちに、「クラスター数」を「2¹（にのいちじょう）」「2²（にのにじょう）」「2³（にのさんじょう）」「2⁴（にのよんじょう）」というふうに飛び飛びに考え、その途中の数は考えないという方策が出てきた。それでもなお、これではマップ全体を方眼紙のように区切ることになって不自然である。（そんなことでよければ何も計算せず方眼の罫を引けばいいのであって「クラスタリング」の出番はない。）ならば「クラスター数」を奇数にすればいい。奇数にしさえすればいいので、それぞれに「＋1」することにした。この「＋1」が気持ちわるいという人もいるかもしれないが、その場合は「府中は特別」「府中以外を数える」という絶対府中宣言「府中がセカイの中心（※当社比）」といったことを表現した数字だと思ってもらうとよい。人数を数えるときに自分を数え忘れる人がいます。

• k=4：3DS版・Switch版ではゲーム自体に「地名」とその区割りを扱う機能がある
• k=5：Switch版（色がすさまじい）
• k=6：3DS版の発想をA9に持ち込んで「地区」の区割りの線を自分で引いている例
• k=11：Switch版（色がすさまじい²：こういう勉強をしてきた人が作っているので「色がすさまじい」とは思っていないだろうが、どう見ても色がすさまじい・色彩を美大で学んだ専門家に（専門家の責任で）やってもらわないといけない＝そうでない人がじぶんでやるのはだめだという認識が必要）
• k=16：3DS版での「地域設定」に区割りの機能があるが、あまり複雑なことはできない
• メーカーとしてはいわゆる「マジカルナンバー7」（ミラーの法則）を意識しているはず：UI設計の基本なのでみんな習います
• k=1（？）：3DS版を未経験だとマップを区割りするという発想自体がない（いわば大ゾーン方式：もちろん大ゾーンにも利点はあります）
• PS2「A列車で行こう2001」では「ステージ選択」というかたちで「大きなマップ」から注目するエリアを選ばせてプレーさせていた：A9のマップ1個を、A2001で選ぶステージの1つのような狭さとは思わず、ステージが10個ある大きなマップだと思ったほうが楽しめるだろう
• 観光用などの地図に表示する注目地点（POI）の数は30程度が限度（昭文社）という人間の認知機能の限界からも「クラスター数」は「k=17」まで考えればじゅうぶん（※1つのクラスターに複数の駅を許す場合の数え方で）ということにしておく
• ゲームのマップ上で直線の区割りをするだけでは硬直的すぎる：「平地」の点群をクラスタリングしていろいろな形に区割りできるのが「府中のメソッド」…と言いたいが、均等に分けるだけなのでこれはこれで硬直的⇒行列の特異値分解を使う「新札幌バウム」にお進みください
• 区割りの線という発想にとらわれすぎてもいけない：リアルな区割りの線を描くことが目的ではなく、だいたいこのへんというクラスターの重心を使う方法である（重心から離れるほど属するクラスターが曖昧）⇒区割りの線をそれらしくしたいときはボロノイ図を
• 先人の肩にだっこにおんぶk-means（k平均法）をそのまま使うことに主眼を置く：k-meansの発想に素直に従う（k-meansではできないことを深追いしない）
• 大昔のBASICで、画面の中央に何かを表示したいとき、表示したいものの大きさと画面の幅から、自分で座標を計算する必要があった（「プロパティ」から「中央揃え」を選ぶだけというものではなかった）：ひたすら平均を計算しまくるk-meansを見ていてちょっと思い出した

もう少し何かしたい

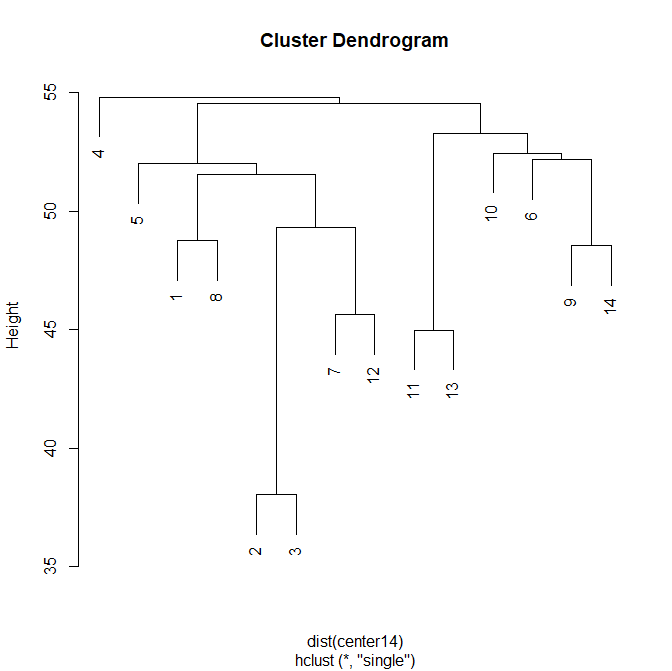
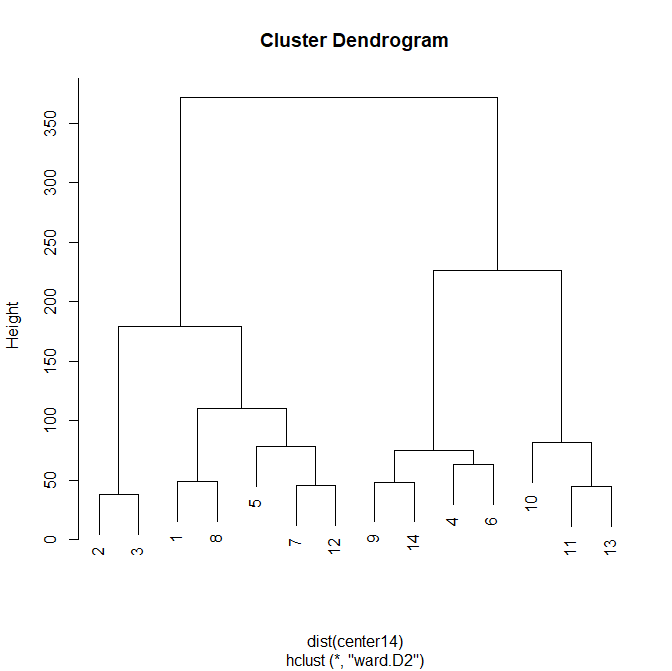
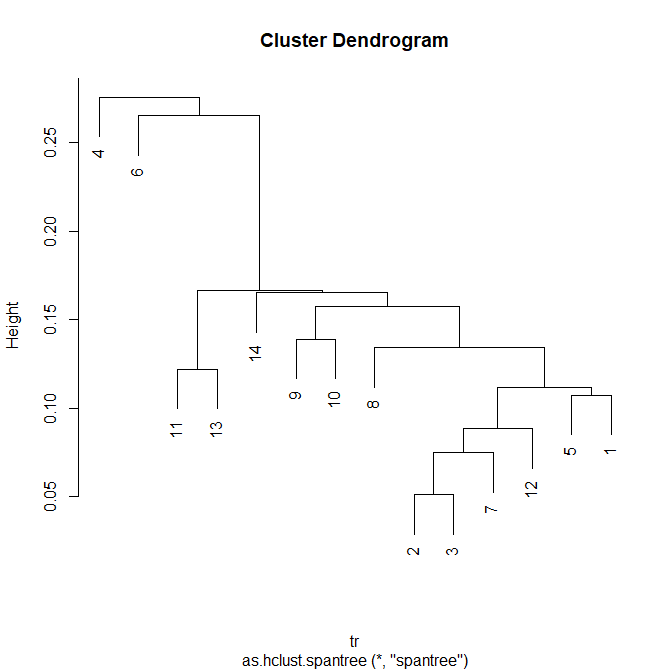
「最近隣法」 「ウォード法」 「最小全域木」 を見比べる
	▲最近隣法 （single）	▲ウォード法 （ward.D2）	▲最小全域木 （spantree）

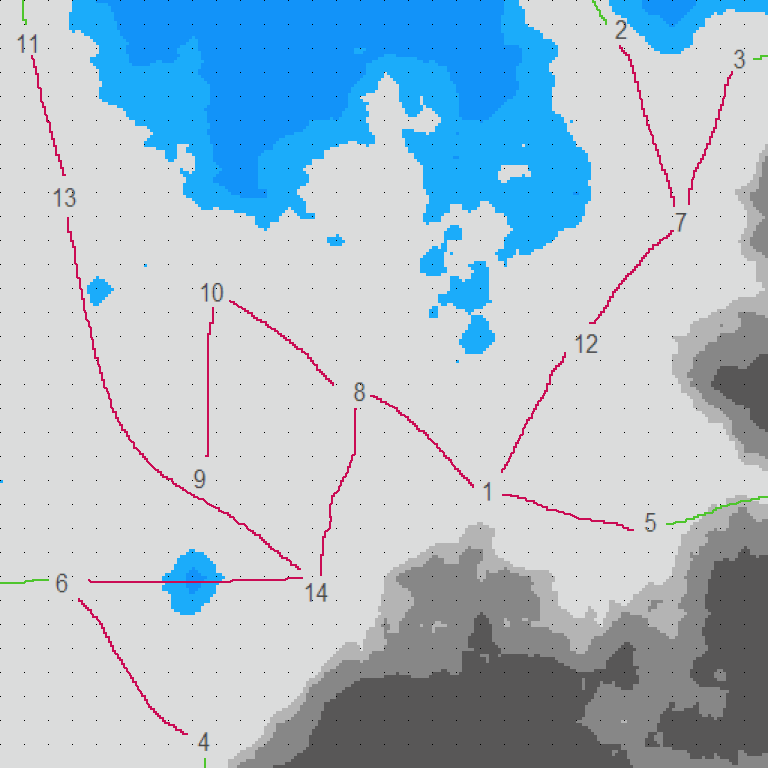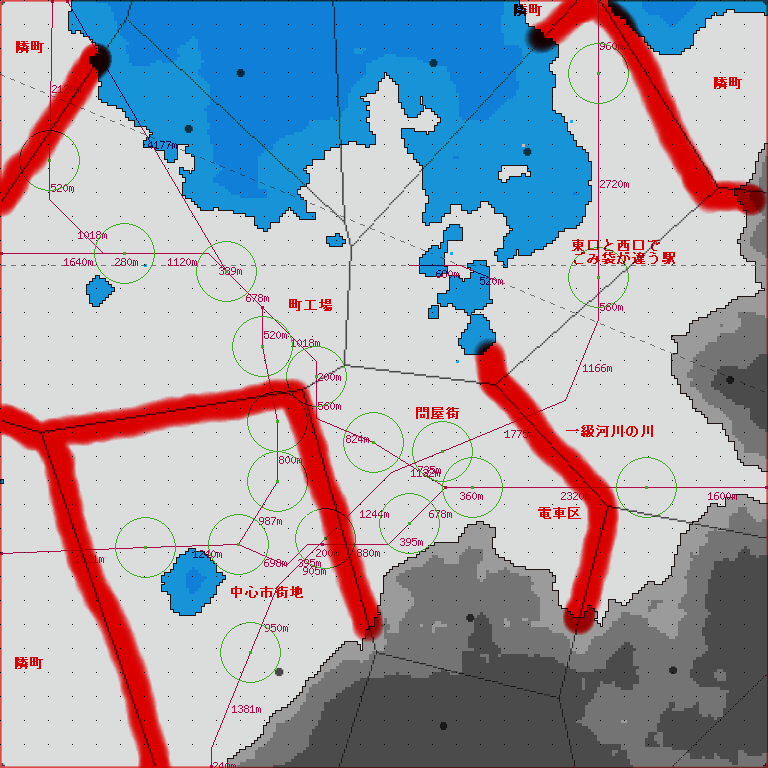
▲最小全域木 （コマンドでプロットするのは… 　挫折した！）	▲ボロノイ図 （…に、裏写りする油性ペン）

• ゲームを開始して最初に引く路線網（※官設鉄道だけのような路線網：1地域1路線で競合がない）を提案する方法として「最小全域木」（左図）が使えそうという感触を得る
  • わざわざ池の真ん中をつっきらなくても…：
    水面を避けるためにクラスター数を非常に多くしてみたらどうだろう
  • 池の真ん中はつっきるくせに行きたいところへまっすぐ行けない：
    k=9で乗換駅の位置を提案し、k=102くらいで（最小全域木でつくった最小限の辺だけを持つグラフで各ノードの固有ベクトル中心性や媒介中心性など複数の指標を求めてからそれを主成分分析して、その第1主成分なりをノードの重みとして使い）経由地を提案したらどうだろう
  • 「最小全域木」というアルゴリズムのほうはそのまま使いながら、データのほうを工夫してみよう
• 平地とは逆に山と水面をクラスタリングしてボロノイ図を描いてみる（右図：Rのスクリプトは「ベクトル円海山」に掲載）
  • この路線網を引いた人間のプレーヤー（※じぶん）に、平地を均等に分割という発想はなかったようだ（※ないです）
  • ボロノイ図の境界の線（ボロノイ辺）が、一級河川の川や、市街地が途切れるところ、隣町のほうから出張ってきた勢力圏のようなものを表わしているような気がしてくるだろう
• このマップの中心地を「府中」と名付けたので「府中のメソッド」と仮称する
  ※府中はすてきな街です。

こちらもお読みください

• あたらしい新逢坂山田前：パッケージ「nnclust」を使って最小全域木（MST）を作る

レトロアクション

このページの方法を考えたときよりも後に考えた方法を、このページで使った地形データに遡及適用してみます。

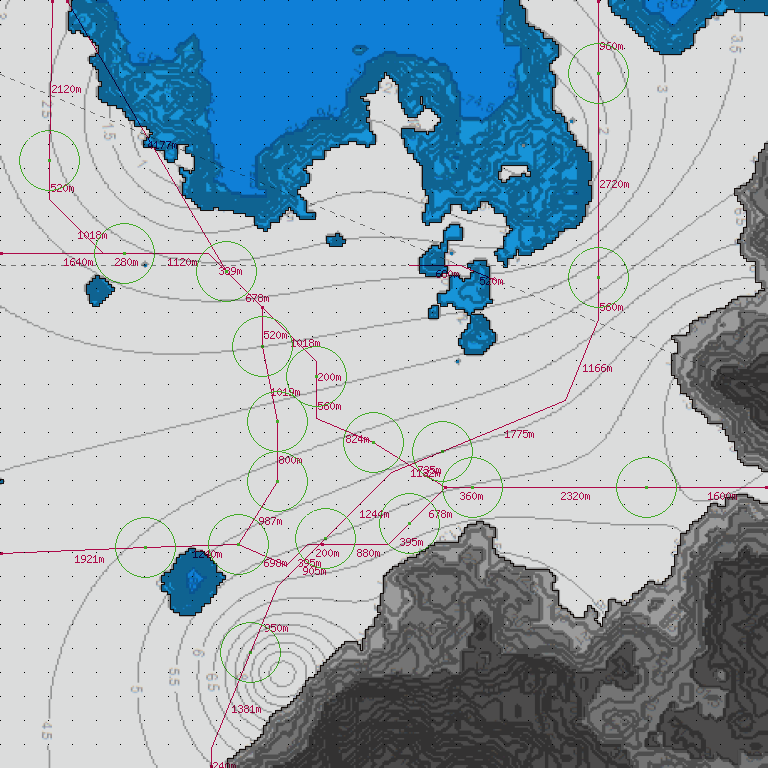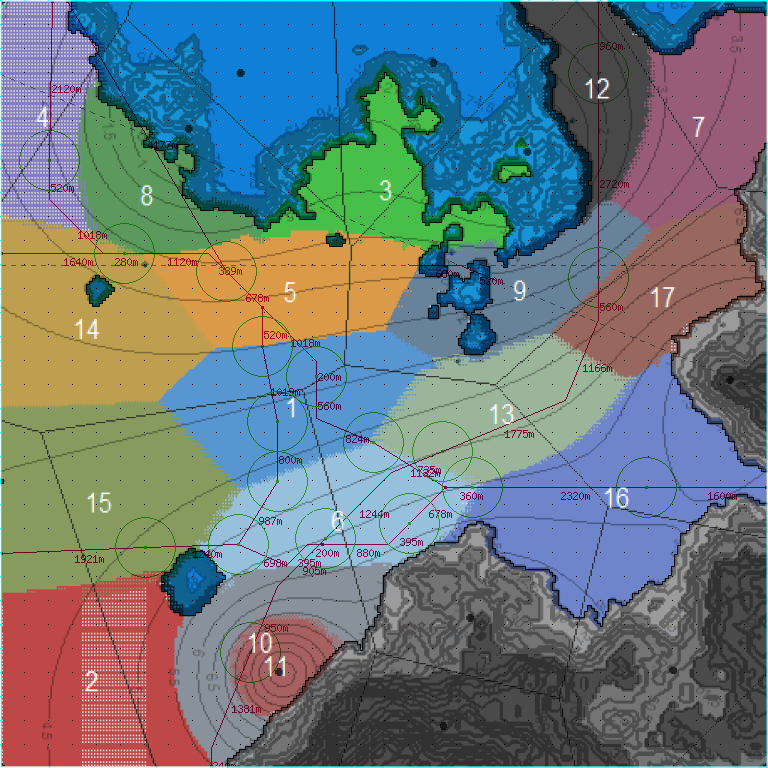▲「ベクトル円海山」	▲「新札幌バウム」

• 多くのプレーヤーがマップの地形を見て何らかの地形上の特徴を読み取って、それを手がかりにして駅や路線の配置を決めていっているはずだと思う：厳しいことを言えば、それができない人を門前払いするゲームになっている⇒アルゴリズムで「ヒント」を提示できればと思う（「ヒント」と呼ぶと「ヒントには頼りたくない」と思われるなら「シナリオ」と呼んでもよい）
• ゲーム「A列車で行こう9」のマップの「平地」そのものには何の手がかりもないので、多くのプレーヤーが自然と「山と水面」に目を向けることと思う（※マップコンストラクションで完全な「平地」に好きなものを好きなように配置していく人を除く）
• 「府中のメソッド」のように「平地」を単純に均等に分割するクラスタリングでは人間のプレーヤーの感覚にそぐわない部分がある（地形をそのように見ないでもないが路線網を考えるときにはほかのことも考慮している）
  1. 「山と水面」を単純に均等に分割するクラスタリングをして、「平地」の「微地形」を復元するのが「ベクトル円海山」（左図）
  2. その「微地形」を主成分分析で回転した空間で、単純に均等に分割するクラスタリングをし、空間を元に戻すのが「新札幌バウム」（右図）
• 「新札幌バウム」による分割は地質の違いに見立てて楽しむことができそう：人間のプレーヤーが直感的に軟弱地盤などを避けて線路や市街地を造った感じをアルゴリズムで模擬できそう
• ゲーム「A列車で行こう9」の中の土地を構成する岩石の成立過程や硬度・粘度などは知りようがないが、大ざっぱには「山」（山体を成す岩盤）に近ければ砂（砂礫）っぽく、「水面」に近ければ泥（堆積物）っぽいと思えばよい：その地点の地質が砂っぽいか泥っぽいかを、山との距離（山の高さを使って重み付け）と水面との距離（水面の深さを使って重み付け）で模擬していることになる（※ものすごく大ざっぱ）
• なお筆者は高等学校の地学を履修していないので地学用語の使用は避ける（いろいろな岩石の名前も体系的には暗記していない）：中学校までの理科に配当された地学的分野が、それはそれでよくできていると実感する（※大ざっぱなことはちゃんと中学校のうちに教えてもらっていて、大ざっぱに考えるだけならそれで足りる）⇒中学校で習う範囲までのことは「常識」扱いできるが高校以上で選択制のものはそうではない（客に要求することになるプレーのための予備知識は中学校までの範囲に限る必要がある）
• ただし右図の「3」の領域は、両隣の「8」や「9」の領域が軟弱地盤であるとしたときに、それとは地質が異なるという想像をすることになる：ゲームとしてプレーしたときには「いわれのある岩場（史跡）」という想像をしてみた
• 「11」の領域は、その近傍の山の急傾斜ゆえ、山の高さによる重み付けが過剰に効いてできたもの：この「11」が、大きいほうの池の成り立ちを説明していそうである
• 「14」にあるほうの池はなぜ小さい？：そこに小さな池ができたのは「地形の自動生成」のアルゴリズムがランダムに加えたノイズにすぎない（現実の地下水のメカニズムを模擬したものではない）が、ナイスな池ができていれば素朴にうれしい
• 「ベクトル円海山」は「微地形の復元」を目指した方法だったが、「微地形」そのものをそれらしく（微地形の成り立ちを模擬して）再現したというよりは、（位置関係だけに基づいて確率的に）地質を説明する意味合いのほうが大きいものとなったと思う
• くれぐれも、これはゲーム「A列車で行こう9」の中で「地形の自動生成」を使用して得られた地形データを対象としたもので、現実の複雑な地形とは異なり明快すぎる結果が出ることに留意：そのことがゲームソフトの新機能やプレーヤーの遊び方にうまく活かせれば、それでよい

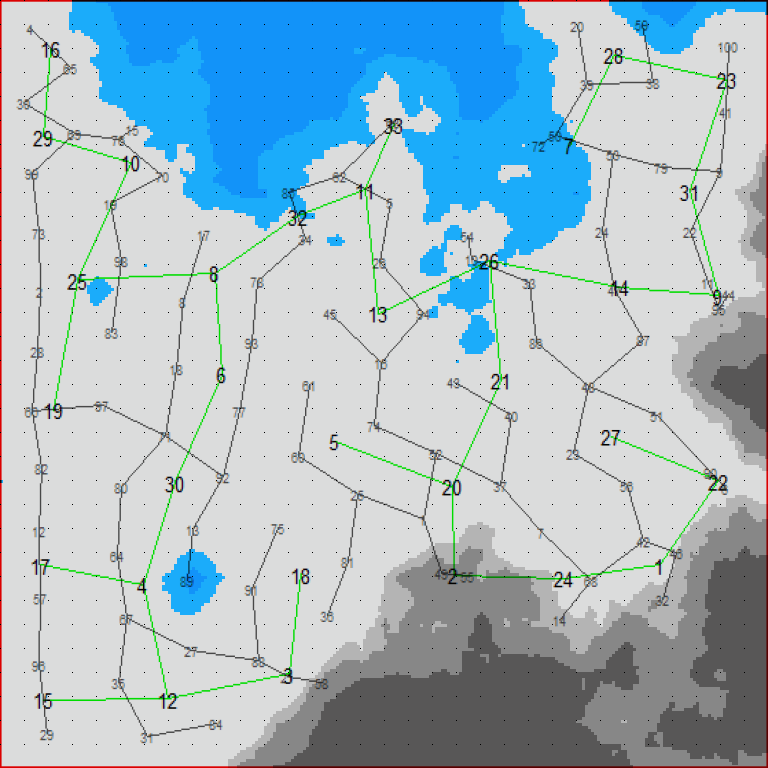▲「適応的新逢坂山田前」 （k＝100・k＝33）

• 「26」の地点は水面だが、マップのみどころとなる複々線以上の長大橋を架けるとよいだろう
• 「20」や「8」「25」「4」の地点は最小全域木（MST）のエッジが3本となり、ターミナル駅（乗換駅）の立地の候補となる
• 最小全域木（MST）の末端となった「27」や「7」は陸の孤島と呼ばれているというストーリーにするとよいだろう

調布のメソッド ～テラマヨス大明神～

	統計数理研究所のミラーサイトから「R」を入手しよう 統計数理研究所とは

ＡＲＸのつまみソース（94359） All Rights Reserved. ©2018-2025, tht.